8 Models for Enzyme Action

1. Objectives

1. To understand the mode of action of enzymes.
2. To discuss different models for enzyme action
3. To understand the mechanism of substrate binding to an enzyme

2.  Concept Map

3.  Description

3.1  Enzymes and their action

Enzymes are remarkable biocatalysts, present in the form of protein or RNA (ribozyme) which accelerate the biochemical reactions under moderate temperature and pressure conditions such that almost all the biochemical reactions require their presence to take place. The specificity of an enzyme depends on the molecular geometry of the substrate thusthe specific enzyme has the ability to catalyze one or a specific class of reactions. The rate of any biochemical reaction depends on many factors such as temperature, pH and enzyme as well as substrate concentration.Gradual increase in temperature, increases rate of reaction, until it reaches optimim temperature range between  250C  to 380C. Increase in the temperature beyond the its optimum range causes0 decrease in rate of reaction due to denaturation of enzyme, as a result it loses its strucural integrity.Despite every enzyme having their own optimal pH value, most enzyme reactions tend to have  higher reaction rates in the range of pH value 6 – 9.

Generally, Mechanism of molecular recognition sounds similar in case of enzyme catalysis, antibody–antigen recognition, protein synthesis, and transcriptional regulation through protein factors and small RNAs. All these cases are characterized by formation of a specific complex when two or more molecules come. Understanding the mechanism that helps molecules recognize each other followed by their interaction with one another will hold universal significance in biological function. In this direction, many of the early studies have pave the way to understand the binding of substrate with an enzyme at specific active site, this understanding further pitch upon the questions as to how an enzyme could perform biochemical reaction so efficiently with greater specificity. These questions were later answered by many of the models for an enzyme action.

3.2   Lock and key model:

In 1894, Emil Fischer proposed a model to explain enzyme function.. This was the first popular model and was known as “Lock and Key theory” (Fischer, 1894). The concept of this theory was attained while working with certain glycolytic enzymes and their abilities to distinguish between different sugar stereoisomers.

Thus the theory behind the Lock and Key model involves the complementarity between the shapes of the enzyme and the substrate. According to this theory, both the enzyme and substrate possess fixed confirmations which allow them to fit easily into one another. The enzyme, capable of accepting one or few substrates represents a ‘lock’ while the substrates are represented as ‘keys’. The substrate has a shape which is complementary shape to its substrate, which allows both enzyme and a substrate to fit like a ‘key’ fits into a ‘lock’. In other words, the enzyme active possesses a geometric shape and orientation which is complementary to that of the substrate. The enzyme and substrate shape do not influence each other. Since both enzyme and substrate already have predetermined perfectly complementary shape, the substrate remains stabilized. The theory offers an explanation for the remarkable specificity of enzymes as it suggests that the enzyme active site is complementary to the reaction ground state (Figure 1).

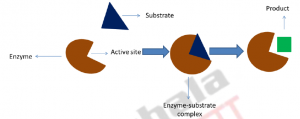
Figure 1: Schematic representation of lock and key model: The model considers the binding of triangular shape substrate to enzyme active site having its complementary shape and forms enzyme substrate complex and lead to release of square shape product from the enzyme.

The major drawback of this model is that it ignores the bound substrate that is transformed to the transition state. At that time, enzymes were considered as carbohydrates and nothing was known about the active site. The theory remained the accepted till 60 years, till Dan Koshland’s induced fit hypothesis was proposed.

In 1930 J.B.S. Haldane for the first time viewed that, the enzymes must be massive molecules (although the concept of proteinaceous nature of enzymes was not been established) and that the chemistry of the enzyme must be confined to a small region, termed as the ‘active site’. According to Haldane’s interpretation, the active site existed in a state which is complementy to the reaction transition state, as its stabilization resulted in rate enhancement. He was also of the opinion that the active site does not exist in a ground state complementarity. The bulk of the enzyme or large mass of the enyme that did not constitute the active site had no active role to play, and was required for the orienting the active site functionalities optimally for binding the transition state.

3.3.   Induced fit hypothesis:

The induced-fit hypothesis depends on the “the conformational plasticity” of enzymes. It has been observed that the active site conformation of an enzyme between the ligand-free and ligand-bound states is different. According to this hypothesis, the interaction between an enzyme and its substrate is said to resemble the fitting of a hand into a glove, wherein the moderately flexible enzyme acts as the glove and fits the moderately flexible substrate (the hand) into it (Figure 2). Three important points are proposed by the model

1. For enzyme activity, a precise orientation of catalytic group is required;
2. Changes in the three dimensional relationship of the active site residues may be brought about by the substrate
3. The changes will be induced by substrate-binding. On the other hand, a non-substrate will not be able to induce these required changes (Koshland 1958).

One of the main arguments that goes against the induced fit hypothesis is that the pathway requires the formation of a Enzyme-subsrate complex 1 which is not favourable thermodynamically (Figure.2). Although the substrates are bound to the enzyme in this complex, the energetically favourable conformational change that is induced by substrate binding is yet to occur. Recent crystallographic studies of at least one enzyme (Sullivan and Holyoak 2008) provide the evidence for the existence of such a conformational state.

This model seemed satisfactory for another 50 years. However in the later part of the twentieth century, the conformational selection hypothesis by Ruth Nussinov (Tsai et al. 1999b) was developed.

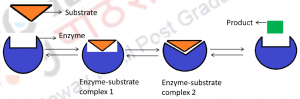
Figure 2: Schematic representation of ‘Induced fit hypothesis’: The substrate binds to enzyme to form the Enzyme-substrate complex 1. Binding of the substrate induces a conformational change in enzyme and leads to the formation of the enzyme -substrate complex 2 which further causes release of a product.

3.4 Conformational Selection Model:

The modification to the induced fit model gave rise to the conformational selection model. Contrary to the induced fit hypothesis, this model does not require the binding event to induce a conformational change in the enzyme. Infact, in this case the binding of a ligand occurs directly to the enzyme, through a mechanism similar to MWC (Monod–Wyman–Changeux) model of cooperativity (Monod et al. 1965). Subsequent to binding, the population of molecules tends to shift towards the active conformation thereby facilitating further binding events (Figure3). This is done in order to maintain equilibrium state between inactive ‘active site’ of an enzyme, active ‘active site’ of an enzyme (active conformation) and bound enzyme with ligand,

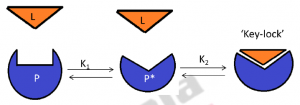
Figure 3: Conformational selection pathway: P (protein) is in a preexisting equilibrium. The active conformation of protein P is P*. Ligand L binds to P* to form the P*-L key–lock complex. As ligand binds to P* , a shift occurs in the population of P toward P* for maintaining preexisting equilibrium between P and P* ( as represented by K1).

As stated above, the conformational selection model is consistent if the enzyme or protein structures are exist as a group of states i.e ligand-bound or lock state is present in the absence of ligand. When there is direct binding of the substrate to the enzyme’s “lock” state, this model is not able to explain why small substrates would be non-substrates for a reaction. An additional aspect which is not addressed by the conformational selection model is that of molecular recognition i.e. binding to enzyme active sites that are either ‘closed’ or ‘open’ in the final “key– lock” state (through conformational change in the active site).

The best model (Figure 4) to explain substrate recognition in enzymes, as well as molecular recognition events came almost 120 years after the initial proposal of the lock-and-key model. This model is a blending of the three hypotheses which have been discuused above.

Figure 4: Molecular Recognition: Lock-and-Key, Induced Fit, and Conformational Selection.

Panel a: Schematic diagram representing the lock-and-key models. In panel B, the induced fit pathwayis defined by the equilibrium constants K1 and K2; the conformational selection pathway is defined by equilibrium constants K3 and K4. In the induced fit pathway, ligand (L) binds to P to form P–L encounter complex. Ligand-binding induces a subsequent conformational change in P and leads to the formation of the P*–L key–lock complex. In the conformational selection pathway, P is present in a preexisting equilibrium with the active conformation P*. Binding of ligand L to P* therefore forms the final P*-L key–lock complex. To maintain the preexisting equilibrium between P and P* (represented by K3), a shift occurs in the population of P toward P*, as ligand binds to P*

Another important mode of action of enzymes is cooperativity, it is the condition that occurs when a particular enzyme contain multiple binding sites in which one of the binding site either activated or deactivated upon binding of a ligand as a result it affects the affinity (decrease or increase) for binding of the other sites. There are two types of cooperative binding; negative cooperativity describes decrease in protein’s or enzyme’s affinity for the ligand when one of the binding sites is occupied by a ligand. a positive coperativity necessitates binding of a ligand to one of the binding sites increases the affinity of binding of a another ligand to the binding sites.

Concerted or MWC model of cooperativity:

MWC model is given by Monod, Wyman and Changeux which shows that, enzyme subunits are arranged in such a way that a conformational change in one of the subunit causes conformational changes in all other subunits which are physically attached to it. Thus all subunits must exist in the same conformation. For example: binding of oxygen  molecule (ligand) to one of the subunit of hemoglobin – a tetramer  causes conformational changes in all the subunits thus brings conformational changes from ‘R’ state to ‘T’ state which occurs in one step (Figure 5).

The T state of the hemoglobin is in the deoxyhemoglobin form and is more tense as the R state of the hemoglobin, present in the oxyhemglobin form is more relaxed. Binding of oxygen molecule on one site tends to increase the binding affinity at other active sites. Equilibrium exists between T-state and R-state at each level of oxygen binding. When other sub units are gradually occupied by binding of oxygen molecule, a shift in the equilibrium occurs from a strongly favoring Tensed-state to a strongly favoring Relaxed-state.

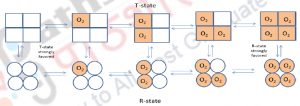
Figure 5: The Concerted Model, also known as MWC model or symmetry model: of hemoglobin which explains the cooperativity in oxygen binding and transitions of proteins made up of identical sub units.

Sequential model of cooperativity:

In this model, binding of ligand causes a conformational change in the sub unit to which it is bound therefore this model says that, unlike in concerted model, sub units are not connected in such a way that a conformational change in one induces a similar change in the other. For example: In hemoglobin, oxygen binding causes conformational change from T-sate to R-state in only one of the monomer to which it is bound, whereas unbound monomers remains at T-state, (Figure 6). In this model, the ligand binding alters the subunit conformation to which it is bound to and also induce changes in the neighboring subunits. In other words, each binding site is able to influence all the binding sites which are nearby until all of the sites are in the same state.It is important to note that either the sequential or the concerted models are not able to fully explain the nature of hemoglobin. Properties from both models appear in a real system.

Figure 6: Sequential model: explains binding of ligand causes conformational changes in one of the monomer to which it is bound and induces the changes in neighboring sub units/monomers.

4.  Summary

In this lecture we learnt about:

• Enzymes and the factors affecting enzyme activity
• Different models for enzyme action